勾股定理是初等几何中的一个基本定理,指直角三角形的两条直角边的平方和等于斜边的平方。勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一,下面是其中一种证明方法。

勾股定理的证明方法
以a、b为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于二分之一ab.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上。 ∵RtΔHAE≌RtΔEBF, ∵ ∠AEH +∠AHE = 90º, ∴ 四边形EFGH是一个边长为c的 ∵RtΔGDH≌RtΔHAE, ∵ ∠HGD +∠GHD = 90º, 又∵ ∠GHE = 90º, ∴ABCD是一个边长为a + b的正方形,它的面积等于a+b的平方。 ∴a的平方加b的平方等于c的平方。 如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形。最长边所对的角为直角。勾股定理的逆定理是判断三角形是否为锐角、直角或钝角三角形的一个简单的方法。若c为最长边,且a²+b²=c²,则△ABC是直角三角形。如果a²+b²>c²,则△ABC是锐角三角形。如果a²+b²<c²则△ABC是钝角三角形。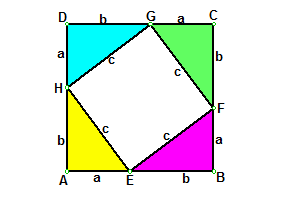
勾股定理的逆定理