2023四川省成都市高三二诊数学试题(理科)

成都市高三第二次诊断性考试 数学（理科）

一、选择题：本大题共12小题，每小题5分，共60分。

1.复数满足（为虚数单位），则的虚部为（   ）

A.                 B.-            C.-1               D.1

2.设全集，集合，，则=（   ）

A.           B.             C.         D.

3.某中学有高中生1500人，初中生1000人，为了解该校学生自主锻炼的时间，采用分层抽样的方法从高中生和初中生中抽取一个容量为n的样本。若样本中高中生恰有30人，则n的值为（   ）

A.20                  B.50                 C.40                  D.60

4.曲线在点处的切线方程为（   ）

A.         B.        C.     D.

5.已知锐角满足，则=（   ）

A.                B.1                 C.2               D.4

6.函数在的图象大致为（   ）

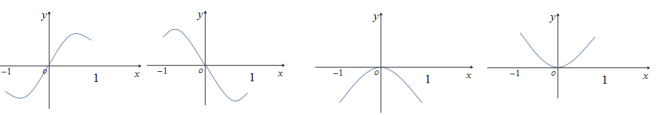
     A                 B                   C                   D

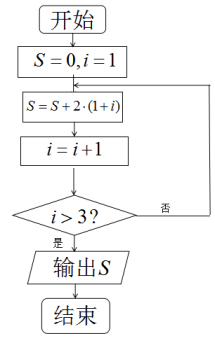
7.执行如图所示的程序框图，则输出S的值为（   ）

A.16              B.48              C.96              D.128

8.已知函数，则函数的图象的对称轴方程为（   ）

A.     B.

C.       D.

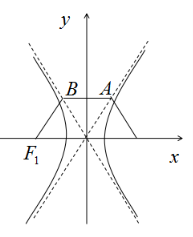
9.如图，双曲线的左，右交点分别是，，直线与双曲线的两条渐近线分别相交于两点.若，则双曲线的离心率为（   ）

A.2              B.            C.              D.

10.在正方体中，点分别为的中点，过点作平面使，若直线，则的值为（   ）

A.               B.              C.           D.

11.已知为圆的一条直径，点的坐标满足不等式组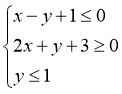，则的取值范围为（   ）

A.           B.              C.               D.

12.已知函数，若存在，使得成立，则的最大值为（   ）

A.               B.                C.                  D.

二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．

13．的展开式中x2的系数为            。

14．在△ABC中，内角A，B，C的对边分别为a，b，c，已知，a=2，b=，则△ABC的面积为            。

15．已知各棱长都相等的直三棱柱（侧棱与底面垂直的棱柱称为直棱柱）所有顶点都在球O的表面上，若球O的表面积为28π，则该三棱柱的侧面积为            。

16．经过椭圆中心的直线与椭圆相交于M，N两点（点M在第一象限），过点M作x轴的垂线，垂足为点E，设直线NE与椭圆的另一个交点为P．则cos∠NMP的值是            。

三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．

17．（12分）已知是递增的等比数列，a1=1，且2a2，，成等差数列．（Ⅰ）求数列的通项公式；（Ⅱ）设，。求数列{bn}的前n项和Sn．

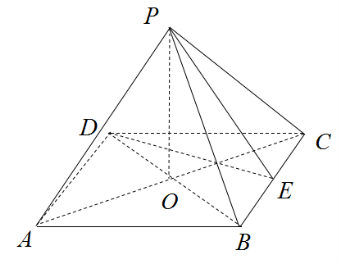
18．（12分）如图，在四棱锥P-ABCD中，O是边长为4的正方形ABCD的中心，PO⊥平面ABCD，E为BC的中点．（Ⅰ）求证：平面PAC⊥平面PBD；（Ⅱ）若PE=3，求二面角D一PE一B的余弦值．

19．（12分）某动漫影视制作公司长期坚持文化自信，不断挖据中华优秀传统文化中的动漫题材，创作出一批又一批的优秀动漫影视作品，获得市场和广大观众的一致好评，同时也为公司赢得丰厚的利润．该公司2013年至2019年的年利润y关于年份代号x的统计数据如下表（已知该公司的年利润与年份代号线性相关）：

（Ⅰ）求y关于x的线性回归方程，并预测该公司2020年（年份代号记为8）的年利润；（Ⅱ）当统计表中某年年利润的实际值大于由（Ⅰ）中线性回归方程计算出该年利润的估计值时，称该年为A级利润年，否则称为B级利润年，将（Ⅰ）中预测的该公司2020年的年利润视作该年利润的实际值，现从2013年至2020年这8年中随机抽取2年，求恰有1年为A级利润年的概率．

参考公式：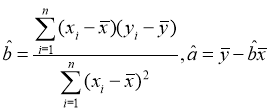

20．（12分）已知椭圆的左，右焦点分别为F1（-1，0），F2（1，0），点P在椭圆E上，PF2⊥F1F2，且|PF1|=3|PF2|．（Ⅰ）求椭圆E的标准方程；（Ⅱ）设直线l：x=my+1（m∈R）与椭圆E相交于A，B两点，与圆x2+y2=a2相交于C，D两点，求|AB|·|CD|2的取值范围．

21．（12分） 已知函数，其中m∈R．（Ⅰ）当m>0时，求函数f（x）的单调区间；（Ⅱ）设，若，在上恒成立，求实数m的最大值．

请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．

22．（本小题满分10分）选修4-4：坐标系与参数方在平面直角坐标系xOy中，曲线C的参数方程为（m为参数）．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线的极坐标方程为．（Ⅰ）求直线l的直角坐标方程与曲线C的普通方程；（Ⅱ）已知点P（2，1）设直线l与曲线C相交于M，N两点，求的值．

23．（本小题满分10分）选修4-5；不等式选讲）已知函数f（x）=|x-1|+|x+3|．（Ⅰ）解不等式f（x）≥6；

（Ⅱ）设g（x）=-x2+2ax，其中a为常数若方程f（x）=g（x）在（0，+∞）上恰有两个不相等的实数根，求实数a的取值范围．

答案

第一卷

1C   2A    3B   4D   5C   6B   7B   8C    9A    10B   11D   12C

第二卷

13.  6      14. 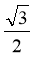    15. 36       16. 0